A legnehezebb feladat olyan dologról összefoglaló munkát készíteni, melynek terjedelme a végtelennel vetekszik, ezért csak egy-egy részletének példáján keresztül lehet annak korszakalkotó jelentőségét felbecsülni. Ezért választottam az építészet bölcsőjének és a matematika szülőhazájának is tekinthető ókori egyiptomi civilizációt.
Az antik görög filozófusok mûveiben is találkozhatunk az egyiptomiak matematikai és építészeti tudományának dicséretével. Arisztotelész Metafizika címû munkájában ezt írja: „ezért jött létre Egyiptomban a matematikai tudomány; ott ugyanis a papságnak megvolt az ehhez szükséges szabad ideje." Hérodotosz görög történetíró, aki leginkább az egyiptomi kultúra gyakorlati oldalát kutatta, a Nílus évenkénti áradása miatt szükségessé váló földmérésekben vélte felfedezni a geometria gyökereit: „Gondolom, ezért találták fel a földmérést, amely azután Hellászba is eljutott." Az atomista Démokritosz is említést tesz a földmérők (harpedomaptoszok - zsinórfeszítők) munkájáról, akiknek legfontosabb mérőeszköze világszerte a kifeszített zsinór volt: „Vonalak szerkesztésében bizonyításokkal senkit sem múlt felül, még az egyiptomiak úgynevezett zsinórfeszítőit sem." Ha már a modern európai kultúra bölcsőjében is ekkora figyelmet szenteltek e kultúrának, bizonyára tanulságos és érdekes emlékeket lelhetünk fel az egyiptomi mûvészet ránk maradt emlékeiben is.
Az egyiptomi kultúra minden bizonnyal legjelentősebb kultúrtörténeti értéket hordozó építményei a piramisok. Ezeket a szent épületeket a halottak újjászületésének vagy megváltásának eszközeként fogja fel. A gúlaformát nemcsak a célszerûség és a technikai fejlődés hozta létre, hanem mélyebb vallási mondanivalója is van ezeknek a síroknak. Maga a porhüvelyt rejtő szarkofág az anyaméhet és a Mindenséget jelképezi. A piramis szó előfordulása az egyiptomi szövegekben „mer", ami az „iar" (felemelkedni) igéből m- praeformatívummal képzett főnév. A piramis szó is egyiptomi eredetû, egy geometriai terminusból, a „per- em- usz"-ból származik, ami valószínûleg a gúla magasságát jelentette. A görög „püramisz" főnév, ami piramist és hegyes cipót jelentett, is ebből ered. A „mer" szócska tehát körülbelül annyit jelenthet, mint a felemelkedés helye; ezt látszik igazolni egy optikai csalódás is, amelyreDobrovits Aladár hívta fel a figyelmet: ha a szemlélő elég közel áll a piramishoz, úgy érzi, mintha az építmény a végtelenbe nyúlna. A későbbi gúla alakú piramisoknál a szimbolikus tartalmak már másodlagossá váltak, módosultak, illetőleg az elvontabb gondolkodást igénylő szoláris eszméknek adták át a helyet, melyek a Napot jelképezték. Héliupolisz (Junu) városában Nap-fétisként őriztek egy szabálytalan alakú hegyes követ, melyet „benbennek" vagy „bennek" neveztek. Ezen kő és a gúla között az egyiptomiak lényegi összefüggést véltek felfedezni, ezért a piramis legszentebb része a csúcs lett. A csúcsokat ritkábban csillogó arany- vagy elektron- (arany-ezüst egyik jelentése fehérarany) lemezekkel vonták be - a hiedelem szerint ide ereszkedik alá a halott fáraó lelke -, így maguk is Napként csillogtak. A piramis magát a fényt is jelképezhette: néhány ábrázoláson a Nap gúla alakjában emelkedik a horizont fölé, tehát a sír azt is igazolni akarta, hogy az égbe jutó megdicsőültnek „Ré" társaságában osztályrésze lesz. Az építmény nem véletlenül volt maga a fényesség, ugyanis az egyiptomiak a napfényt parányi háromszögekből álló szubsztanciának képzelték el, ezért az anyagban realizálódott monumentális háromszögek csak úgy válhattak fénytermészetûvé, ha valamilyen nemesfémmel bevonták őket. Egyes antik szerzők az előbbi felfogás miatt azt képzelték, hogy a piramisoknak nincs árnyéka. Összességében a piramis látványa kettős élményt nyújt: a felemelkedés és a lesüllyedés, a kicsúcsosodás és a szétterjedés érzetét kelti.

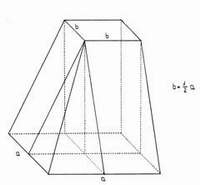
Két hasáb a moszkvai papiruszból. Csonka gúla térfogatának kiszámítása; alapélek: 2, illetve 4 könyök, magasság: 6 könyök. Fent: a hieratikus szöveg; lent: J. J. Perepjolkin hieroglifikus átírása, melyet V. V. Sztruve közöl. A szöveg a következőképpen szól: 1. Add össze ezt a 16-ot 2. ezzel a 8-cal és ezzel a 4-gyel: 3. kijön 28. Számítsd ki 4. 1/3-át a 6-nak. Kijön 2. 5. Számolj 28-asával kétszer. Kijön 56. 6. Nézd, ez 56. Helyesen számítottad ki. A hieroglifikus szöveget jobbról balra kell olvasni. A fedőlap oldala (2) és annak négyzete (4) felül a rajzon van feltüntetve, az alapél (4) alul, a magasság (6) és a térfogat (56) pedig a rajz belsejében. 28-nak 2- vel való szorzása a rajztól balra látható.

A legnagyobb „igazi" piramisokat a IV. dinasztia idején (körülbelül Kr. e. 2626-2585) emelték Gízában Hufu és Menkauré (ismertebb nevükön: Kheopsz, Khephrén és Mükerinosz) fáraóknak. Kheopsz piramisa egy kb. 147 méter magas, hatalmas temetkezőhely központja. A piramis architektúrája szem előtt tartotta az ősi csillagállást: a bejáratot következetesen északon helyezték el, ugyanis az asztrális túlvilághit tanítása szerint a léleknek az égbolt északi pólusának régiójába kell eljutnia, „a pusztulást nem ismerő" (cirkumpoláris - egész évben a horizont felett tündöklő) csillagok közé. Az egyiptomi matematika két legfontosabb ránk maradt emléke a Rhind-papirusz és a Moszkvai Matematikai Papirusz. Mindkét jelentős matematikatörténeti emlék a középbirodalomból való, pontosabban a Rhind-Papirusz középbirodalmi eredetije alapján készült." Ezt az iratot a 33. uralkodási évben, az áradás évszak 4. hónapjában (őfelsége Felső- és Alsó-Egyiptom királya, Aausszeré (Apóphisz) alatt - aki élettel legyen megáldva - másolták régi iratok alapján. Készíttetett Felső- és Alsó-Egyiptom királya, Nimaatré alatt (III. Amenemhat) Jahmesz írta ezt a másolatot." (A. B. Chace-L. Bull-H. Parker Manning: The Rhind Mathematical Papyrus. Oberlin, 1929. I. tábla.) A mértani feladatokat is megőrző papiruszok alapján megállapítható, hogy a tízes számrendszerben dolgoztak. Egytől kilencig a számokat vízszintes, illetve függőleges vonalakkal jelölték (például: 3 = III. A tízeseket a halom Ç jelezte, a százasokat a zsinórral , az ezreseket a lótuszvirággal , a tízezret az ujjal, a százezret az ebihallal , a milliót és az ettől nagyobb számokat a feltartott kezû emberalakkal fejezték ki. Ezeknek a jelöléseknek az volt a hátránya, hogy a jelek leírása meglehetősen bonyolult volt, és nagyobb számoknál rendkívül sok jelet kellett leírni, ami sok időt vett igénybe. Analitikus szemléletüknél fogva a görbe vonalak pontjait derékszögû koordináta-rendszer segítségével határozták meg. Merőlegesek kitûzésére felhasználták azokat az összefüggéseket, amelyeket később a görög matematika Pythagoras- tételnek nevezett el. A szögeket hosszadatokra bontották, s tulajdonképpen a cotangens trigonometriai szögfüggvénnyel dolgoztak. Hosszmértékeiket az emberi test arányaival határozták meg: hét tenyér szélesség alkotta az egyiptomi rőföt (53,2 cm); az egy rőf magasságban, tenyérszélességgel mért visszaugrás határozta meg a piramis hajlásszögét és a hasonló háromszögek között fennálló összefüggések alapján meg tudták határozni a kifaragandó burkolókövek formáját. A törtek közül csak a kétharmadnak és a háromnegyednek volt külön jele, egyébként csak olyan törteket alkalmaztak, melynek számlálója 1 volt (a nevezőt az r hieroglifa alatt tüntették fel).

Egy 9 egység átmérőjû, 10 magasságú csûr térfogatát a következő módon számították ki - a mai V = r2 p · m összefüggéssel ellentétben: „Vond le kilencből a kilenced részét, vagyis 1-et, a maradék nyolc. Szorozd meg 8-cal, ez lesz 64. Szorozd meg 10-zel a 64-et, ez lesz 640. Add hozzá a felét, ez 960. Ez lesz az ûrtartalma „harban" (1,5 köbrőf = 1 har)". (I. m. 67. tábla, 41. feladat.) A fenti számítás képletekkel leírva a következőképp fest: amelyből kitûnik, hogy a p Egyiptomban közelítőleg 3,1605 volt. Továbbá a háromszögek területét is viszonylag pontosan meg tudták határozni (a háromszögek, téglalapok és trapézok esetén a ma elfogadott képleteket használták): a háromszög alapját két részre osztották, „hogy a háromszög derékszögûvé tessék", majd szorozzák a magassággal. A trapézok területét az egyik ma is érvényben lévő területképlet alapján számították ki: a párhuzamos oldalak összegét szorozták a magasság felével. A félgömb felszínének és különböző térfogat-számítási problémák kiszámítására is kidolgozott mûveletekkel rendelkeztek, de az egyiptomi geometriának minden kétséget kizáróan a legnagyszerûbb teljesítménye a négyzet alapú csonka gúla térfogatának a Moszkvai-Papiruszon olvasható tökéletes kiszámítása. A térfogatot képlet alapján számították, ahol „h" a magas - ságot, „a" az alapélt, „b" pedig a fedőlap oldalát jelölte. Ennek a rendkívül komplikált képletnek a kidolgozása egészen biztosan nem empirikus úton zajlott. Ha a gúla köbtartalmát felbontjuk egy „b" alapélû, „h" magasságú négyzetes hasábra, két „b" magasságú, háromszög alapú hasábra és egy gúlára, ekkor a térfogat a képlettel számolható ki. Ez a gondolatmenet azonban meghaladná az egyiptomiak képességeit, így elképzelhető, hogy a térfogatot csak olyan gúláknál tudták teljes pontossággal meghatározni, melyeknél a fedőlap oldala az alapél fele. Valószínûsíthető, hogy a korabeli egyiptomiak ismerték a számelmélet alapelemeit. Az egyik piramis sírkamrájának falán olvasható a 2520 szám. Ha kiszámítjuk az első tíz természetes (nem nulla) szám legkisebb közös többszörösét, pont 2520-at kapunk; ebből arra következtethetünk, hogy az első tíz szám mindegyikének volt valamilyen misztikus tartalma.

A piramisépítő technikát mind a mai napig homály fedi. A 2000 évvel később élt görög történetíró - Hérodotosz - a következőket jegyzi meg Kheopsz piramisának építéséről: „Kheopsz olyan mérhetetlenül gonosz volt, hogy amikor már pénze elfogyott, saját leányát bordélyházba küldte és ráparancsolt, hogy szedjen össze neki bizonyos mennyiségû ezüstöt ... arra kényszerítette népét, hogy neki dolgozzék. Az egyik részének megparancsolta, hogy az arábiai hegység kőbányáiból kőtömböket vonszoljon egészen a Nílusig; a másik részének azt a munkát adta, hogy a folyamhoz szállított köveket továbbvigye egészen a líbiai hegységig. Hozzávetőleg 100 ezer ember dolgozott állandóan, háromhavonként felváltva egymást. A sanyargatott nép tíz esztendei munkájával készült el az az út, amelyen a köveket vonszolták. Véleményem szerint sokkal kisebb alkotás ez, mint maga a piramis ... csupa csiszolt kőből készült, melyeket vésett alakok díszítenek ... Magának a piramisnak a felépítése húsz évig tartott. A piramis alapja szabályos négyszög ... simára csiszolt, faragott, igen pontosan összeillesztett kőtömbökből áll... A piramis lépcsőzetesen készült... Amikor az első lépcsőzet elkészült, a többi követ rövid fagerendákból szerkesztett gépezetekkel emelték fel... Először a piramis felső részét fejezték be, azután a szomszédos, alatta lévő részeket és végül az alapot és a legalsó részeket." Hérodotosz elképzeléseinek ellentmond az a tény, hogy az akkori Egyiptomban még nem ismerték az emelőcsigát, ezért biztos, hogy nem használtak emelőgépeket. A közelmúltban Dick Parry angol mérnök egyszerû és nagyszerû magyarázata nagy vihart kavart az egyiptológusok körében. Õ is a „csigaelvet" használja fel magyarázatában, holott a Nílus menti építőmesterek kezdetben még nem ismerték a mai kereket és kocsit.Az ásatások során előkerült több olyan körszeletre hasonlító „libikóka", amelyeknek egyik oldala egyenes, a másik pedig egy kör negyed íve. Ha négy ilyen libikókát összeillesztünk, egy korongot kapunk. Két ilyen koronggal felszerelve a kőtömböket a piramiskezdemény oldalához épített rámpán viszonylag könnyen mozgathatók. (25%-os lejtésû rámpán a kb. 2,5 tonna súlyú kőtömbök 18 ember munkájának eredményeként kevesebb mint egy perc tizenöt másodperc alatt 15 méterrel magasabbra gördíthetők.) Az építkezés során a belső tereket homokkal töltötték ki, párhuzamosan az épület emelkedésével. A felületek végső kidolgozását fentről lefelé haladva kezdték el, mert a kőtömböket már a fejtés helyén megpróbálták megfelelő méretûre vágni és faragni. A tömböket a helyszínen olyan pontosra alakították ki, hogy a köztük lévő rész - kötőanyag nélkül is - még a hajszál átmérőjénél is kisebb volt. A legfelelősségteljesebb feladat az építészre hárult, akinek nemcsak az épület tájolását kellett a rendelkezésre álló csillagászati eszközökkel kijelölnie és a felmerülő technikai problémákra megoldást találnia, hanem az építkezés ideje alatt különböző rituális szertartásokat kellett végeznie. Egyes kutatók a Kheopsz piramis méreteiben titokzatos összefüggést vélnek felfedezni: szerintük ezek a számok őrzik a egyiptomiak tudományát; sőt más áltudományos összefüggéseket alkotók a Földnek a Naptól való távolságát, atomsúlyokat vélnek kiolvasni belőlük. A piramisokat kétségtelenül magas intelligenciájú kultúra hozta létre, de ismereteik nem lehettek azonosak a jelenkor tudományáéval. Egyiptom, ez a természet legmostohább, legszélsőségesebb körülményeinek kitett ország megmutatta a világnak és az utókornak, hogy szigorú munkaszervezéssel, összefogással, a rendkívül kezdetleges tudományos ismeretek összerakásával csodákra képes. A társadalom szigorúan hierarchikus felépítése biztos alapját képezte a világtörténelem egyik legnagyobb, legszilárdabb és a mai kor emberének is tekintélyt parancsoló kultúrájának.